Ranger's Way

Algorithm -- Binary Tree to Linked List (In-place)

Flatten a Binary Tree to Linked List, with preorder, inorder, or postorder. Implement the algorithm in place.

I’ll use 3 different methods to implement each order. They are [recursion with TreeNode, void recursion, iteration].

I’ll remember this problem for I had lost a great opportunity without solving it.

And also remember, don’t reference only one or even only two solutions when cracking LeetCode. And an alternative as well as most essencial point is cracking it with your own codes.

Flatten Binary Tree to Linked List is the preorder problem.

Void Recursion

Inorder

First, let’s talk about inorder!!!

This is the simplest method. We use similar codes while traversing a Binary Tree with void recursion. Assuming no requirement of in place implement. Then we can simply append every traversed TreeNode in the tail of a Linked List.

e.g. Inorder version without requirement of in place, which takes a static LinkedList as result.

static LinkedList<TreeNode> list = new LinkedList<TreeNode>();

void flattenInorder(TreeNode root) {
  if (root == null) return;
  falttenInorder(root.left);
  list.add(root);
  flattenInorder(root.right);
}

Then, the list is the result, you can treat it as a cache which stores the output of inorder traverse while System.out.println(root.val); is being used instead of list.add(root).

Now, let’s compare the above with the in place algorithm, which takes constant (two: prev & head) number of variables.

static TreeNode prev = null;
static TreeNode head = null;

void flattenInorder(TreeNode root) {
  if (root == null) return;
  flattenInorder(root.left);
  if (head == null) head = root;
  if (prev != null) {
    prev.right = root;
  }
  root.left = null;
  prev = root;
  flattenInorder(root.right);
}

Then, the head is pointing at the begining of the flattened Linked List.

If you do not like to use static, you can create another function void flattenInorder(TreeNode root, TreeNode[] prev, TreeNode[] head with prev[0] and head[0] for passing reference of previous node and head node of Linked List.

TreeNode flattenInorder(TreeNode root) {
  TreeNode[] prev = new TreeNode[1];
  TreeNode[] head = new TreeNode[1];
  flattenInorder(root, prev, head);
  return head[0];
}

void flattenInorder(TreeNode root, TreeNode[] prev, TreeNode[] head) {
  if (root == null) return;

  flattenInorder(root.left, prev, head);

  root.left = null;
  if (prev[0] != null) {
    prev[0].right = root;
  }
  prev[0] = root;
  if (head[0] == null) {
    head[0] = root;
  }

  flattenInorder(root.right, prev, head);
}

Preorder

Like the simple tree traverse, we can use a similar code structure to flatten a Binary Tree into Linked List with preorder.

  • As the root of BT is the head of LL, we do not need to set head pointer.

  • As the right pointer of each node will be set before recusion called on rightBranch, so we need to set a variable to mark rightBranch in every recursion.

    void flattenPreorder(TreeNode root, TreeNode[] prev) {
  if (root == null) return;

  TreeNode rightBranch = root.right;
  if (prev[0] != null) {
    prev[0].right = root;
  }
  prev[0] = root;

  flattenPreorder(root.left, prev);
  root.left = null;
  flattenPreorder(rightBranch, prev);
}

Postorder

  void flattenPostorder(TreeNode root, TreeNode[] prev, TreeNode[] head) {
    if (root == null) return;

    flattenPostorder(root.left, prev, head);
    if (head[0] == null) {
      head[0] = root;
    }
    flattenPostorder(root.right, prev, head);

    root.left = null;
    root.right = null;

    if (prev[0] != null) {
      prev[0].right = root;
    }
    prev[0] = root;
  }

From the 3 different order of void recursion, we can see that:

if (prev[0] != null) {
  prev[0].right = root;
}
prev[0] = root;

Theses code snip is similar to the print current node sentence in tree traverse: println(root.val);.

Iteration

The iteration traverse of Binary Tree is commonly implemented with an assistant Stack. But in this quesiton, we are required to use constant space, so we should take advantage of the left/right pointers.

Inorder

TreeNode flattenInorder(TreeNode root) {
  TreeNode head = null;
  TreeNode last = null;
  while (root != null) {
    if (root.left != null) {
      TreeNode pre = root.left;
      while (pre.right != null) {
        pre = pre.right;
      }
      pre.right = root;
      pre = pre.right;
      root = root.left;
      pre.left = null;
      if (last != null) {
        last.right = root;
      }
    } else {
      if (head == null) head = root;
      last = root;
      root = root.right;
    }
  }
  return head;
}
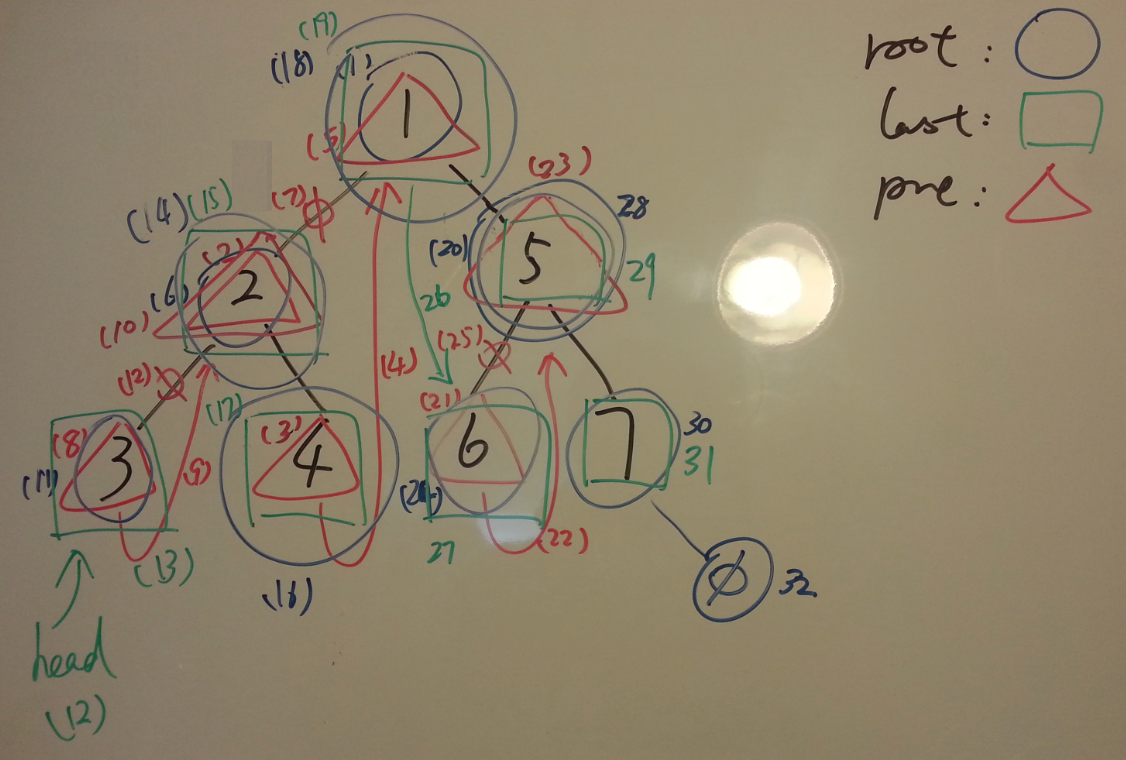
  • TreeNode pre is used to mark the previous node of the root when root’s left child is existed;
  • TreeNode last is used to traverse Linked List after head has been set.

This shows inorder iteration of flatten, the data stream is labled by (index) in colors.

inorder iteration of flatten

Preorder

The preorder iteration is obviously the most simplest way to flatten a Binary Tree to a Linked List.

void flattenInorder(TreeNode root) {
  while (root != null) {
    if (root.left != null) {
      TreeNode prev = root.left;
      while (prev.right != null) {
        prev = prev.right;
      }
      prev.right = root.right;
      root.right = root.left;
      root.left = null;
    }
    root = root.right;
  }
}

Postorder

How?

Recursion with Return Value

The signature of recursion with return value is TreeNode flatten(TreeNode root) { ... /* recursion */ ... }.

The tricky part is we are attempting to use this single one recursion to impelment the entire flatten function. So we need to reture the head of Linked List. It will be relatively easier for preorder. But harder for the other two types.

Inorder

Actually another simple problem could be solved by Divide-and-Conquer, just need to reserve the left pointer while recursion rather than set null.

Hinted by in place convert a Binary Tree to Doubly Linked List

This version requires to

  • track left pointer while recursion;

  • reset the head of Linked List and set left pointer to null after recursion.

    TreeNode flattenInorder(TreeNode root) {
  // build inorder doubly linked list
  root = flattenInorderHelper(root);

  // set head
  while (root.left != null) {
    root = root.left;
  }

  // set left null
  TreeNode p = root.right;
  while (p != null) {
    p.left = null;
    p = p.right;
  }

  return root;
}

TreeNode flattenInorderHelper(TreeNode root) {
  if (root == null) return null;

  if (root.left != null) {
    TreeNode left = flattenInorderHelper(root.left);
    while (left.right != null) { left = left.right; }
    left.right = root;
    root.left = left;
  }

  if (root.right != null) {
    TreeNode right = flattenInorderHelper(root.right);
    while (right.left != null) { right = right.left; }
    right.left = root;
    root.right = right;
  }

  return root;
}

Preorder

This non-trivil version is too tricky for me.

TreeNode flattenPreorder(TreeNode root) {
  if (root == null) return null;
  TreeNode tail = root;
  TreeNode right = root.right;
  if (root.lleft != null) {
    tail = flattenPreorder(root.left);
    root.right = root.left;
    tail.right = right;
    root.left = null;
  }
  if (right != null) {
    tail = flattenPreorder(right);
  }
  return tail;
}

or

TreeNode flattenPreorder(TreeNode root) {
  if (root == null) return null;

  TreeNode rightTree = root.right;
  if (root.left != null) {
    root.right = null;
    root.left = null;
    root = flattenPreorder(root.right);
  }
  if (rightTree != null) {
    root.right = rightTree;
    root = flattenPreorder(root.right);
  }
  return root;
}

Postorder

This is my own trivial version of postorder followed by the inorder version.

Two pointer should be taken care for:

  • Set root.right = null to avoid infinite loop in recursion;

  • When linking right pointer, if root.right == null, the next (right) pointer of last node (most right node in left branch) should be linked to root directly.

    TreeNode flattenPostorder(TreeNode root) {
  root = flattenPostorderHelper(root);

  // set head
  while (root.left != null) {
    root = root.left;
  }

  TreeNode p = root.right;
  while (p != null) {
    p.left = null;
    p = p.right;
  }

  return root;
}

TreeNode flattenPostorderHelper(TreeNode root) {
  if (root == null) return null;

  TreeNode leftTree = root.left;
  TreeNode rightTree = root.right;
  root.right = null;
  if (leftTree != null) {
    leftTree = flattenPostorderHelper(leftTree);
  }

  if (rightTree != null) {
    rightTree = flattenPostorderHelper(rightTree);
  }

  if (leftTree != null) {
    while (leftTree.right != null) { leftTree = leftTree.right; }
  }
  if (rightTree != null) {
    TreeNode rightFirst = rightTree;
    while (rightFirst.left != null) { rightFirst = rightFirst.left; }
    leftTree.right = rightFirst;
    while (rightTree.right != null) { rightTree = rightTree.right; }
    rightTree.right = root;
  } else {
    if (leftTree != null)
      leftTree.right = root;
  }

  return root;
}

Reference

1. http://www.geeksforgeeks.org/in-place-convert-a-given-binary-tree-to-doubly-linked-list/
2. http://www.geeksforgeeks.org/convert-a-given-binary-tree-to-doubly-linked-list-set-2/
3. http://www.geeksforgeeks.org/convert-given-binary-tree-doubly-linked-list-set-3/
4. http://leetcode.com/2010/11/convert-binary-search-tree-bst-to.html
5. http://cslibrary.stanford.edu/109/TreeListRecursion.html
6. http://www.geeksforgeeks.org/in-place-convert-a-given-binary-tree-to-doubly-linked-list/
7. http://n00tc0d3r.blogspot.com/2013/03/flatten-binary-tree-to-linked-list-in.html

Category: Technology 33

Tags: algorithm 11 java 5 BinaryTree 1 LinkedList 1

点击查看评论