Ranger's Way

LeetCode Question -- Word Ladder II

题目来源: LeetCode OJ, Word Ladder II

思路简介: 先用BFS找出最短路径，在Word Ladder I的基础上修改，使BFS遍历到的word按遍历先后层级排列；然后用DFS找出所有可能的最短路径。

Question:

Given two words (start and end), and a dictionary, find all shortest transformation sequence(s) from start to end, such that:

  1. Only one letter can be changed at a time
  2. Each intermediate word must exist in the dictionary

For example,

Given:
start = "hit"
end = "cog"
dict = ["hot","dot","dog","lot","log"]

Return

  [
    ["hit","hot","dot","dog","cog"],
    ["hit","hot","lot","log","cog"]
  ]

Note:

  • All words have the same length.
  • All words contain only lowercase alphabetic characters.

Analysis:

这个问题从Word Ladder I的基础上演变而来。Word Ladder I相对简单，只需求出两个单词间的最短路径即可。普遍的做法使用BFS。而这个问题则要求__所有可能的最短路径__。

II的解法也有很多种，但是却不容易[AC]通过，主要原因是时间复杂度太大： 造成时间复杂度过大的可能有两个原因：

原因1. 在字典很大的情况下，Word Ladder I也有相同原因，即与其遍历整个Set<String> dicts，不如在当前word string的基础上把每个char分别尝试替换为[a-z]，总共遍历长度是word.length() * 26；可能远远小于遍历整个字典所需要的时间。
(题外话：我称这种为小学生思路，因为我觉得如果让一个小学生来做这类题目，他们可能往往想到的就是这种最朴素的解决办法。而由于大部分程序员的思路会受到刷题训练的限制，往往想到iteration就是用while或者for loop来遍历，而忽略了看似简单幼稚，实则可能更实用的解法)

原因2. 第二个超时原因就在于具体如何找出__所有的__最短路径的方法上了;

原因3. 在以上两个解决的前提下，可能还需要用到DP Cache来保存结果避免重复计算。

我的想法是这样的：

(1) 在__原因1.__解决的前提下，既然用BFS去寻找第一条最短路径是肯定不会超时的，那么如果我用一个时间复杂度不大于BFS的算法去找出所有路径，也不会超时；

(2) 我先想到了DFS，但是还不知道如何应用DFS去解决。我先在纸上画出了BFS的队列模型，试着找出线索。

看一个稍微复杂点的例子：

start = hit
end = cog
dict = [hot,dot,dog,lot,log,dof,mit,sit,set,mog,mig,seg,nax,max]
</p>

Return

  [["hit","hot","dot","dog","cog"],
   ["hit","hot","lot","log","cog"],
   ["hit","mit","mig","mog","cog"]]

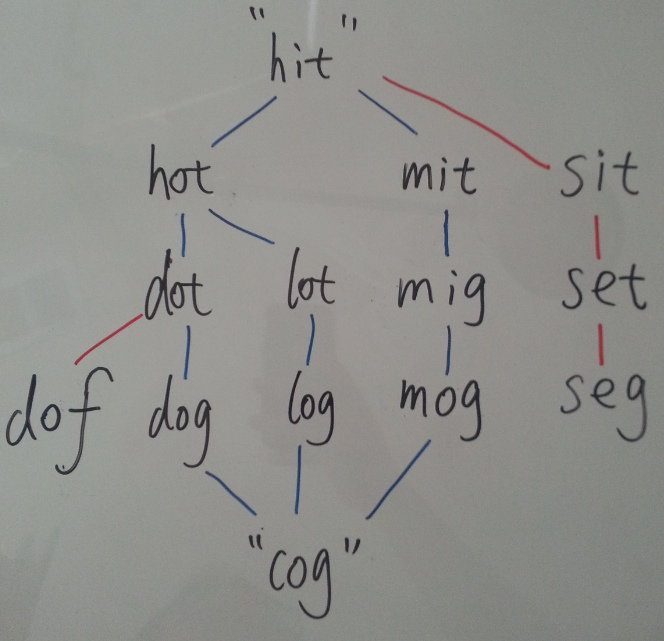
word ladder bfs level

蓝色的线表示valid（可以连通start -> end），红色的线表示invalid。其中，”nax”和”max”这两个单词均未遍历到。

可以发现BFS遍历到的word是有层级先后顺序的：

level 1: [hit]
level 2: [mit, sit, hot]
level 3: [mig, set, dot, lot]
level 4: [mog, seg, dof, dog, log]
level 5: [cog]

在建立了这个样个BFS层级结构的基础上，不难想到最短路径就是在每一层level中选一个word组成的。这里就可以用DFS来解决了。

到这里初步的想法成型了，还有两个需要想清楚的问题：

(1) 字典中其他尚未遍历到的单词，比如”nax”和”max”，如何处理，是否可以被忽略？ 必要性
是。这些单词有两种情况，”nax”和”max”是属于同一种情况，他们不参与任何形成start -> end的路径；还有一种情况，比如加入一个单词”sog”，那么便有一条长度为6的路径[hit,sit,set,seg,sog,cog]，但是这条路径由于超过了最短路径长度5，所以”sog”可以被忽略。

(2) BFS建立的层级结构，它包含了所有可能构成最短路径的word吗？ 充分性
能。但是需要在Word Ladder I的基础上修改，防止一找到路径就结束程序。而是要继续找出同一层级中的其他word，倒数第二层(end 前一层)上的word都有可能是构成最短路径的最后一步。

Code:

程序有点长，分为4个方法

两个辅助方法:

  • String changeChar(String s, int i, char c) 替换String s中位置为i的char为c；
  • boolean canTransform(String s1, String s2) String s1是否可以更改一个char变为s2。

两个主要方法：

  • List<List<String>> findLadders(String start, String end, Set<String> dict) 主函数，包含BFS建立层级结构的实现，和调用DFS返回结果；

  • List<List<String>> dfsPathDP(List<List<String>> levels, int level, String start, String end, HashMap<String,List<List<String>>> cache) DFS遍历：List<List<String>> levels是BFS建立的层级结构，int level是当前层级数，String start是上一层level所选择的word，String end是最短路径终止word，HashMap用来做DP Cache。

    class WordLadderII_Refact {
  static List<List<String>> findLadders(String start, String end, Set<String> dict) {
    List<List<String>> res = new ArrayList<List<String>>();

    if (canTransform(start, end)) {
      List<String> path = new ArrayList<String>();
      path.add(start);
      path.add(end);
      res.add(path);
      return res;
    }

    List<String> bfs = new ArrayList<String>();
    int level = 1;
    int begin = 0;
    /* a HashMap could be both 1) track explored and 2) length calculate
     * but we alread have `Set<String> dict` to track the explored */
    HashMap<String, Integer> explored = new HashMap<String, Integer>();
    bfs.add(start);
    explored.put(start, 0);
    dict.remove(start);
    dict.remove(end);

    List<List<String>> levels = new ArrayList<List<String>>();

    int minLength = -1;
outer:
    while (begin < bfs.size()) {
      if (minLength >= 0) { //!!!
        break;
      }

      int tail = bfs.size();
      // add new level list
      if (levels.size() == level - 1) {
        levels.add(new ArrayList<String>());
      }

      for (int i = begin; i < tail; i++) {
        String curr = bfs.get(i); // get(i)
        for (int j = 0; j < curr.length(); j++) {
          for (char c = 'a'; c <= 'z'; c++) {
            String s = changeChar(curr, j, c);

            //!!! dict Set MAY NOT include "start & end"
            if(s.equals(end)) { //!!! FOUND min path
              explored.put(end, level);
              minLength = level + 1;

              levels.get(level-1).add(end);
              break outer;
            }

            if (dict.contains(s) && !explored.containsKey(s)) {
              explored.put(s, level);
              dict.remove(s);
              bfs.add(s);
              // add s into its level
              levels.get(level-1).add(s);
            }
          } // end of inner for
        }
      } // end of outer for each level
      level++;
      begin = tail;
    } // end of while

    if (minLength == -1) {
      return res;
    }

    /* DFS DP */
    HashMap<String, List<List<String>> > cache = 
      new HashMap<String, List<List<String>> >();
    return dfsPathDP(levels, 0, start, end, cache);
  }

  static List<List<String>> dfsPathDP(List<List<String>> levels, 
      int level, String start, String end,
      HashMap<String,List<List<String>>> cache) 
  {
    if (cache.containsKey(start)) {
      return cache.get(start);
    }

    if (level == levels.size()) {
      if (start.equals(end)) {
        List<String> pathEnd = new ArrayList<String>();
        pathEnd.add(end);
        List<List<String>> endRes = new ArrayList<List<String>>();
        endRes.add(pathEnd);
        cache.put(start, endRes);
        return cache.get(start);
      } else {
        return null;
      }
    }

    List<List<String>> res = new ArrayList<List<String>>();

    List<String> currLevel = levels.get(level);
    for (String s : currLevel) {
      if (!canTransform(start, s)) {
        continue;
      }
      List<List<String>> tailingRes = dfsPathDP(levels,
        level + 1, s, end, cache);
      if (tailingRes == null) { //!!!
        continue;
      }
      for (List<String> path : tailingRes) {
        List<String> newPath = new ArrayList<String>();
        newPath.add(start);
        newPath.addAll(path);
        res.add(newPath);
      }
    } // end outer for

    cache.put(start, res);
    return res;
  }

  static String changeChar(String s, int i, char c) {
    StringBuilder sb = new StringBuilder(s);
    sb.setCharAt(i, c);
    return sb.toString();
  }

  static boolean canTransform(String s1, String s2) {
    /* a very simple version cause string is determined in length */
    int diff = 0;
    for (int i = 0; i < s1.length(); i++) {
      if (s1.charAt(i) != s2.charAt(i)) {
        if (diff == 0) {
          diff++;;
        } else {
          return false;
        }
      }
    }
    return true;
  }

  public static void main(String[] args) {
    String start = "hit";
    String end = "cog";
    Set<String> dict = new HashSet<String>();
    String[] dictArray = new String[]{"hot","dot","dog","lot","log","dof","mit","sit","set","mog","mig","seg"};
    for (String s : dictArray) {
      dict.add(s);
    }

    List<List<String>> res = findLadders(start, end, dict);
    System.out.println(res.size());
    for (List<String> path : res) {
      System.out.println(path);
    }
  }
}

以上就是我的代码，我觉得我的代码在coding上和思路上都还有优化的余地。

Coding上的优化可以是在BFS建层级结构那段，我用了比较不常用的outer loop标记；

思路上可以优化的部分是DFS，我在遍历DFS时，实际重复计算了boolean canTransform(String s1, String s2)。

这题还要注意一些edge cases，比如：start wrod 和 end word 可能在Set<String> dict中，也可能不在dict中。

Also see:

zsxwing / leetcod-java

Yu’s Coding Garden

“一亩三分地”上也有讨论这个问题的帖子

Category: Technology 33

Tags: algorithm 11 java 5 leetcode 1 graph 1

点击查看评论